一、卡尔曼滤波简介KF
卡尔曼滤波器(Kalman Filter)是一种用于估计动态系统状态的递归算法。它通过结合系统的动态模型和噪声观测数据,提供对系统状态的最优估计。卡尔曼滤波器广泛应用于信号处理、控制系统、导航、计算机视觉等领域。
卡尔曼滤波器基于线性系统模型,假设系统的动态过程和观测过程都受到高斯噪声的影响。滤波器在两个主要步骤之间交替进行:
预测(Prediction):根据系统的动态模型,利用前一时刻的状态估计来预测当前时刻的状态和协方差矩阵。
更新(Update):结合当前的观测数据,对预测的状态和协方差进行校正,得到改进的状态估计。
- 应用
- 导航和定位:在GPS和惯性导航系统中,用于实时估计位置、速度和姿态。
- 信号处理:用于滤除信号中的噪声,提取有用信息。
- 控制系统:在自动控制系统中,用于估计系统状态,提高控制精度。
- 计算机视觉:在目标跟踪和物体识别中,用于估计物体的位置和速度。
- 经济学和金融学:用于时间序列分析和预测经济指标。
1.1 卡尔曼滤波核心思想
滤波(Filtering)是一种用于处理信号或数据的技术,其目的是从原始数据中提取出所需的信息并去除噪声、误差或不相关的信息。卡尔曼滤波结合了系统的动态模型和传感器测量数据,通过递归地更新估计状态来提供对系统状态的最优估计。它通过最小化状态估计的均方误差来优化估计结果,因此被称为最优滤波器。
卡尔曼滤波的核心思想是:假定观测的系统是线性的,噪声都满足高斯分布。这一刻系统的状态(最优估计)是这一刻的预测值和这一刻的测量值的加权平均,当得到最优估计之后,再将这一刻的最优估计和估计值进行对比,如果相差比较小,则说明估计比较准确,下次计算就加大估计值的权值,否则说明估计值不准确,下次计算就加大测量值的权值。重复以上过程。
卡尔曼滤波算法的本质,就是基于数值的不确定性调节这个参数K(卡尔曼增益)。在迭代若干次后逼近输出值不确定性最小的数值。当前值=K预测值+(1-K)观测值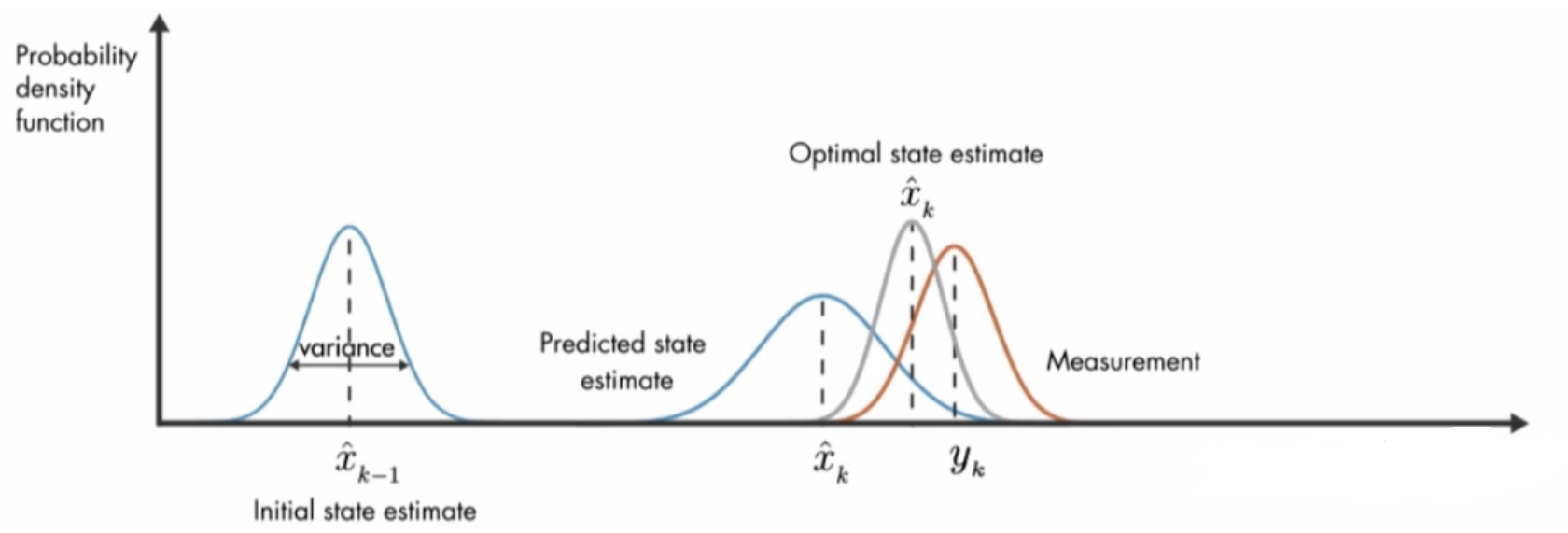
1.2 卡尔曼滤波公式推导
宏观理解
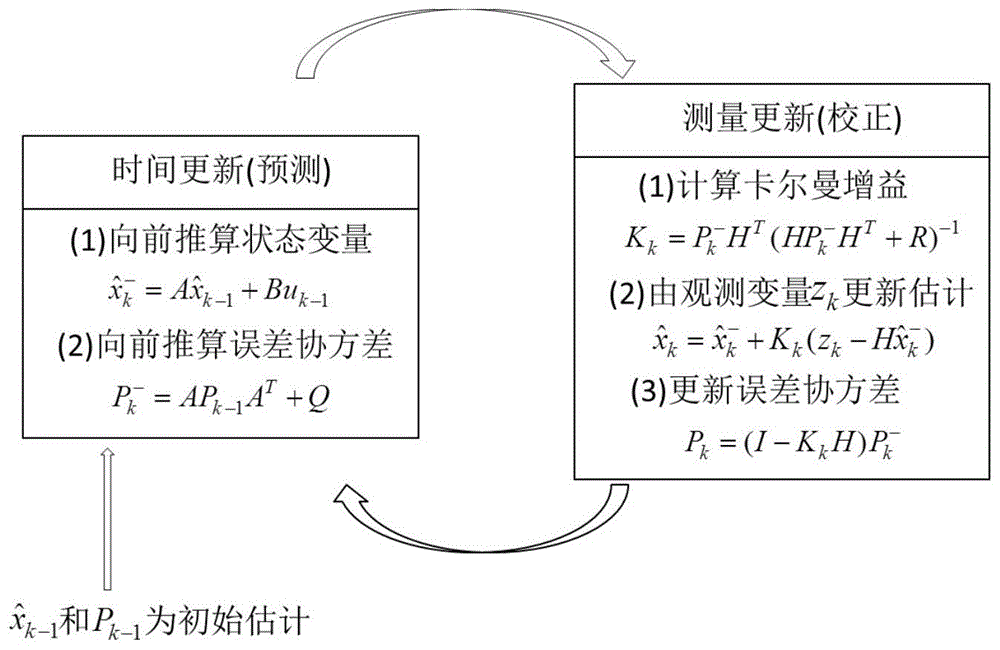
卡尔曼滤波分为预测和更新两步
1.使用上一时刻的最优结果预测当前的值
2.使用当前时刻的观测值修正
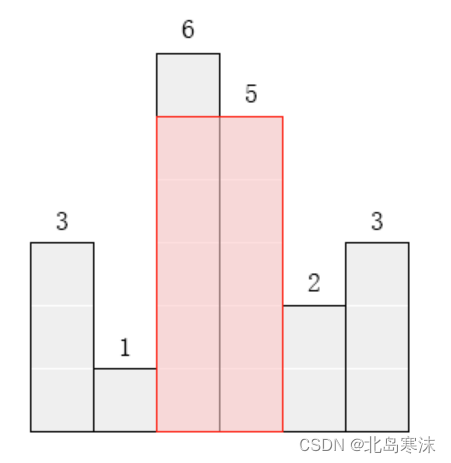
5个核心公式的关系如下图所示
- 公式1:基于过去时刻的状态以及控制量对当前时刻的状态进行估计,注意,数据是先验的。
- 公式2:计算公式1的先验估计状态的协方差矩阵,前一部分是由上次最优估计值自身引入的协方差,后一部分是本次估计产生的不确定性(比如无法预测的外部扰动以及模型自身的不确定性)。
- 公式3:计算卡尔曼增益(参数K),这个参数决定了相信估计值还是相信测量值多一些。
- 公式4:就是根据公式4的卡尔曼增益计算得到的最优状态估计值公式5:计算本次最优状态估计值的协方差矩阵,这个数据在下一次迭代的公式2中被用到。
1.3 公式推导
下面通过一个例子,明白卡尔曼滤波公式的原理,假设一个匀加速行驶的小车,由卫星GPS的值,估计出小车的速度和位置
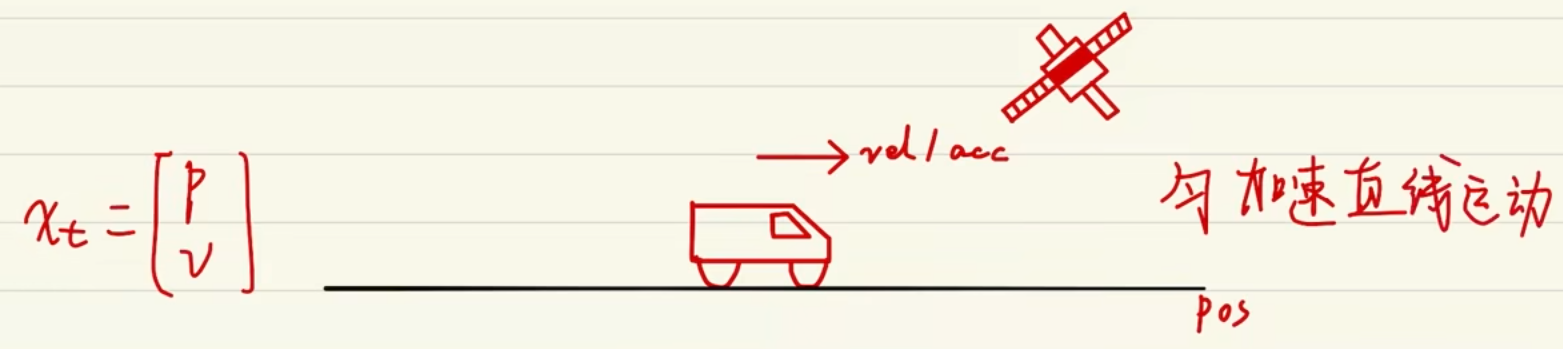
详情请见...
从零入门激光SLAM(十六)——卡尔曼滤波基础 - 古月居 (guyuehome.com)
视频请见..
放弃(通俗公式理解)_哔哩哔哩_bilibili